Matrix structural analysis
OVERVIEW


The Matrix Structural Analysis solution is also called Finite Element Analysis, or the Displacement Method, or  the Stiffness Method (as opposed to the Flexibility Method.) 

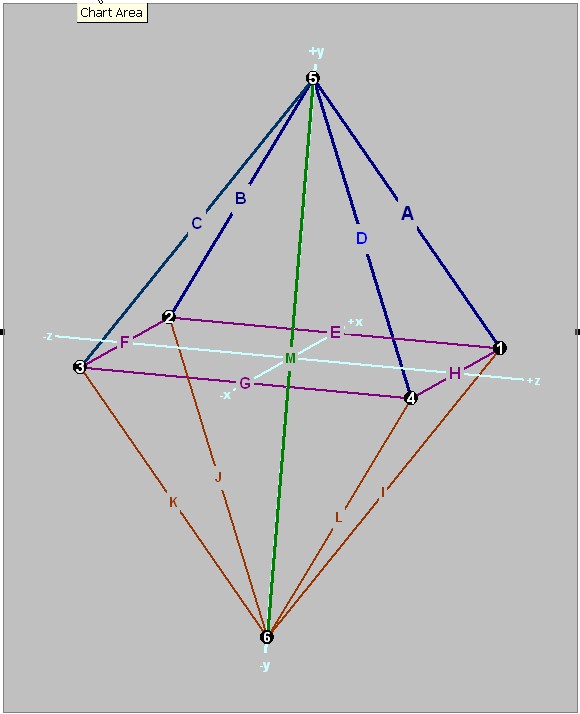
The system consists of nodes (specific locations in a Cartesian coordinate system), and  elements (structural members) that connect the nodes.  All nodes in a structural system must be connected to a least one element, and all elements must be connected to a least two nodes.

The coordinate system defining the nodes is called the Global Coordinate System.  It is the common coordinate system to which all the element local coordinate systems must be resolved in order to effect a solution.    

Each element has its own Local Coordinate System.  Internal forces and deformations (deflections and rotations) in their local coordinate system are related to the global coordinate system by means of the Transformation Matrix. 

External loads are applied to nodes only. 

 
In a Nutshell This section presents the development of the matrix equations (in abbreviated format) from beginning to end. Its purpose is to give the student and practitioner a bird' eye view of the entire process. 

S = Ls CTL k LT C LsT W
Pinned Rods This section presents the development of the pinned rod, and then illustrates its use in a structural system.


Beams This section presents the development of the beam, and then illustrates its use in a structural system.

UnderConstruction
Panels This section presents the development of a panel, and then illustrates its use in a structural system.

UnderConstruction
Plates This section presents the development of plate, and then illustrates its use in a structural system.

UnderConstruction

Matrix Algebra

 This section is a review of the matrix algebra that is used in matrix Structural Analysis.

UnderConstruction